
Lug Dimensions: Height of hole centreline, H = Width of Lug, W L = Radius of Lug, R = Diameter of Hole, DH = Thickness of Lug, tL = Allowable Stresses: Lug Material Allowable Tension Stress, 0.6 x Fy = Allowable Shear Stress, 0.4 x Fy =
20000 kgs = 1 2.0 60 degrees 40,000 kgs =
44,092 lbs
88,184 lbs
120 mm = 300 150 60 28
4.72 inch
mm = mm = mm = mm =
11.81 5.91 2.36 1.10
A 36 Fy = 1,519 Kg/cm2 = 1,012 Kg/cm2 =
inch inch inch inch
36,000 psi 21,600 psi 14,400 psi
DH/2R = 0.20 Stress-Concentration Factor (near hole), K = 2.5 (for flat plate with centrally located circular hole in tension based on DH/2R value)
Tension Stresses in the Lug: Weight in each Lug, W = Cable Tension at Lug, F = Inertia Moment of Lug, IL = Stress at Lug to Beam Joint = ST = F.cos (q). H.(W L/2)/IL +
40,000 kgs = 46,188 kgs = 6,300 cm4 = 1,136 Kg/cm2 =
F.sin(q)/(W L.tL) Stress at near the hole = ST = K .F. sin (q) / [(2.R -DH).tL]
88,160 lbs 101,798 lbs 151.36 in4 16,153 psi Safe
Ratio =
Safe
21,160 psi Ratio = 97.96%
Safe
3,909 psi Ratio = 27.15%
Safe
4,887 psi Ratio = 33.93%
1,488 Kg/cm2 =
74.78%
Shear Stresses in the Lug: Stress at Lug to Beam Joint = SS = F.cos(q) / (tL.W L)
275 Kg/cm2 =
Stress at near the hole = SS = F.cos(q) / [(2.R - DH).tL]
344 Kg/cm2 =
Page 5
Stresses in Weld: The calculation used is conservative as it only includes top fillet welds (actual stresses are lower) Leg size of fillet weld, LW = use 45 degree fillet weld Throat size of fillet feld, tW =
17.68 mm =
0.70 in
Length of weld, Ww1 = 2.W L + 2.tL
656.0 mm =
25.83 in
1,743.4 mm =
68.64 in
530,330 mm3 =
32.36 in3
Length of weld including welding in web of beam, W
25.0 mm =
0.98 in
W w2 = W w1 + W L + 2.Hbeam Section Modulus of weld lines, SW = SW= tw.W L2/3 Efficiency of weld, n = Allowable Load on weld Tension Stress at the weld = ST=[F.cos(q).H/SW+ F.sin(q)/ (W w2.tw)] / n Shear Stress at the Weld = ST=[ F.cos(q)/ (W w1.tw)]/ n
100% 675 Kg/cm2 =
9,600 psi
652 Kg/cm2 =
9,276 psi Safe
Ratio =
Safe
2,832 psi Ratio = 29.50%
30.86 Kg/cm2 =
96.62%

5.4 2-Hook lift factors 23 5.5 Dynamic amplification factors 24 5.6 Skew load factor (SKL) 25 5.7 Additional factors 27 5.8 2-Part sling factor 27 5.9 Lift stability 27 6 DERIVATION OF HOOK, LIFT POINT, AND RIGGING LOADS 28 6.1 Introduction 28 6.2 Hook loads 28 6.3 Lift point loads 29 6.4 Sling loads 29.

Lifting Lug Design Calculation Pdf
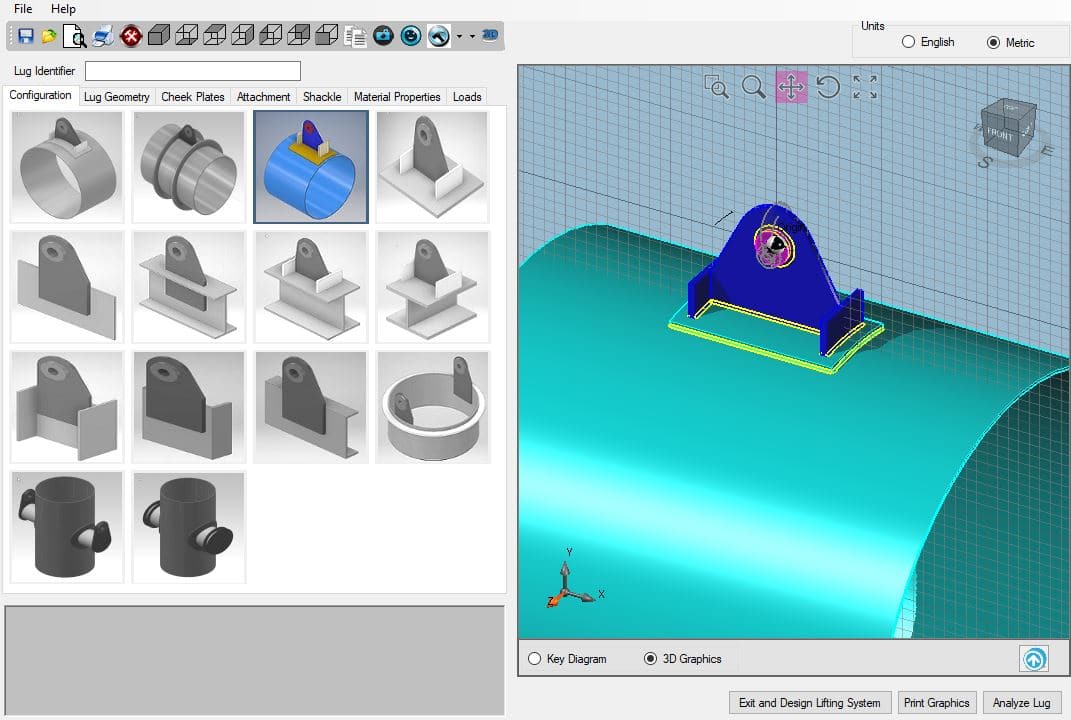
Lifting Lug Design Calculation Pdf
.Lifting and rigging. A crane is designed to lift a load by using ropes or chains. The load must be properly attached using a rigging system. There will definitely be a couple questions on the PE exam about lifting and rigging so make sure to do multiple practice questions. Left of the lug plate, it can actually be either way and the calculations are still valid. EXAMPLE 1: A plate lug used to lift a skid. The printout below shows the design for a plate lug without any side load, but it is the basis for calculating the additional stress that a side load imposes on a plate lug and the weld. This section describes the types of pad eyes (also called lugs) and the technical requirements for lifting operations. A demonstration of the lifting terminology is shown in Fig. Three main types of design geometries for pad eyes are described in NORSOK R-002 lifting stand - ard 1. A lug, also known as a lifting lug or a padeye, is essentially a plate with a hole in it where the hole is sized to fit a clevis pin. Lugs are used in combination with clevis pins to transmit load between different mechanical components. Common applications where lugs are used include.